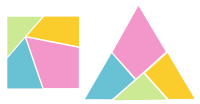藍色情懷

The Haberdasher's Problem, created by Henry Dudeney.

將一正三角形切割成四塊然後重新組合為一正方形。

在此，將分類整理的項目加以概述，必要時加上例圖。

基本上將三角形分為兩大類：

第一類是任意三角形。

第二類是特殊條件的三角形，如等腰、直角、正三角形等等…。這些三角形因其在某些特殊情形下，會產生和任意三角形不同的結果。

由於範圍太廣，在此只討論特殊條件三角形中的正三角形，其餘會在正方形分割翻轉成三角形之逆推的單元中提到。

不論是哪一類，因須將切割部份翻轉使之重合，才能拼成另一完整之幾何形狀，所以必須在三角形兩邊中點連線的設計架構下，建立矩形（如圖2-1-1之DEFG）和平行四邊形（如圖2-1-2之DEFG）兩種基本分割模式，以下推論才能成立。

圖2-1-1

圖2-1-2

亦即，三角形分割翻轉重組必要條件如下：（如圖2-1-3）

1. D
、E為三角形兩邊中點。Þ  則AD=BD、CE＝BE。
2. 線段
DE/ / AC、且線段DE＝1/2×AC＝FG。

矩形為基本形，其分割模式是最簡易的。以下說明皆以下圖2-1-3為依據標準。

圖2-1-3

在三角形分割翻轉重組上，除了分析翻轉重合之必要性外，尚須考慮翻轉後預期形狀之特性，如此才能根據其特性做適當的設計分割，如：

1. 預期幾何形狀為－－矩形時
，其頂點特性為四角皆90°，且兩邊不等長。因此在頂點位置上，我就必須將它們設在矩形DEFG兩對頂點D、F在對角線EG上之垂足即得（如圖2-1-4）。




圖2-1-4

2. 預期幾何形狀為－－梯形時
，其頂點特性構成上下兩邊平行且不等長。因此在頂點位置上，我就只須將它們設在矩形DEFG之對角線上任意點即可，但不可為中點（如圖2-1-5）。




圖2-1-5

3. 預期幾何形狀為－－平行四邊形時
，其頂點特性構成兩雙對邊平行且不等長。因此在頂點位置上，我就只須將它們設在一為除與矩形DEFG對角線之一半長度相等之交點外，任取一點I，另一為相互平行線段之交點H即可（如圖2-1-6）。




圖2-1-6

4. 預期幾何形狀為－－菱形時
，其頂點特性構成兩雙對邊平行且等長。因此在頂點位置上，我就只須將它們設在兩對角線相交之點H即可（如圖2-1-7）。

圖2-1-7

諸如此類……。

所以我尚須分析分割頂點在四邊形DEFG之位置性質。而分割頂點在四邊形DEFG之位置可分為：在矩形內、在矩形邊上。其在矩形內頂點型式或在矩形邊上型式又可分為：對角線交點（如圖2-1-3之H點）、對角垂足（如圖2-1-4之H、I兩點）、DE中點或其他特定點（如圖2-1-5之H點為對角線上任一點）等。

在三角形分割翻轉重組設計上，第一基本分割模式──矩形，無法滿足預期的幾何形狀，因而第二基本分割模式──平行四邊形法（如圖2-1-8）就成為必要考慮。以下說明皆以下圖2-1-8為依據標準。

圖2-1-8

有些四邊形必須要用平行四邊形分割模式才能設計成功，如正三角形變正方形即是（此在正三角形分割為正方形之迷思與驗證討論的單元中會再討論），有些只能在矩形分割模式下才能設計成功，如鴛形（如圖2-1-9），又有些是矩形分割模式及平行四邊形分割模式皆可設計出來，如平行四邊形（圖2-1-10、2-1-11）、矩形、梯形、菱形…等。

圖2-1-9

圖2-1-10矩形分割模式

  圖2-1-11平行四邊形分割模式

在下單元中將提到的正三角形翻轉為正方形案例，這是一個令人著迷的益智幾何問題！就是和矩形分割模式很相像的平行四邊形分割模式，普通人極為容易混淆，下單元會有詳細的解說。

將一正三角形切割成四塊然後重新組合為一正方形：

圖2-2-1

 參考資料: Martin Gardner, More Mathematical Puzzles and Diversions, p. 26

其中提到的正三角形切割成四塊然後重新組合為一正方形，此亦為美國數學家Harry Lindgreen於其著作〝Geometric Dissections〞中證實為最少分割塊，當時我也有以AutoCAD製作圖形，並把它歸類到矩形分割模式中，因此不免對這份文件多看幾眼，但越看越是納悶，因其並沒有說明其設計和分割方法，使我再一次深入探討所繪製的圖形是否與之為同一類，但越是檢查越覺得疑點重重，首先我將繪製的正三角形翻轉成正方形的圖形叫出來，並以AutoCAD設正三角形邊長為a=50，再用其中的尺寸標註工具來檢驗正方形邊長長度，且將尺寸精度設定最高後，發現其邊長一為b=33.07189139，另一為c=32.73268354，差距極小，因此外觀上四邊形HJKL極易讓人誤以為正方形，其實是矩形，驚訝吧！（如圖2-2-2）

圖2-2-2

如要用幾何的方式證明也會得到同樣的結果：

因為 線段JK＝HL＝HE＋EL＝GE＝DF

 線段KL＝JH＝2DH＝DH＋IF

圖2-2-3

由附圖2-2-3，因為直角三角形DHO和IFO全等且斜邊大於另兩股，由此可看出，線段DF＞DH＋IF，故可得知線段JK＞KL。

原本推算到此，以為網路上的圖形有問題，於是引發我找出正確圖形的動機，所以利用其不論如何分割翻轉面積都一樣的特性為根據：

圖2-2-4

前面提到，正方形邊長JK＝HL＝GE，因此就想辦法將GE等於上面求出的正方形邊長，為了求得G的正確位置，我以E為圓心，上面求得的正方形邊長為半徑，畫圓，交AC於G，而G`為D在AC上之垂足，兩者並不相同且差距極小（若a＝50，則只差GG`＝0.22538084），肉眼極難分辨，F則是過E點而平行於DG的線段與AC線的交點，而F`為E在AC上之垂足，故□DEFG為平行四邊形。

我也用幾何的方式再證了一遍：

線段JK＝HL＝HE＋EL＝HE＋IE＝HE＋GH＝GE

證明：JH＝HL

• 故所得之 □HJKL為正方形。

於是得到：要將正三角形分割翻轉成正方形，其基本分割模式是平行四邊形而非矩形。但是他們的差距微乎其微。由於網路所查得資料沒有標明作圖方法，單用肉眼又看不清楚，無法判斷它是矩形或平行四邊形，一般人很容易造成誤解而不知，這也就是本研究所謂的迷思與陷阱！

↑圖2-2-5 圖2-2-6↓

圖2-2-5和圖2-2-6是正三角形分割翻轉成正方形的可行性，只是它使用的方法和我不一樣，但目的都是一樣的，也就是找出他圖中Ｉ的正確位置（亦即我圖中G的正確位置），得到這一點後，才能進一步的達到正三角形分割翻轉成正方形的正確圖形。

它一開始的方法和我一樣：（如圖2-2-5）

設正三角形邊長BC＝2，高h＝√3，△ABC面積＝翻轉後的正方形面積＝2×√3÷2＝√3，翻轉後的正方形邊長＝⁴√3。亦即翻轉後的正方形邊長＝FE＋GE＝FE＋IF＝IE，得這樣的結果後，就可以：

以E為圓心，⁴√3為半徑，交BC於I，就可找到正確的分割翻轉方式。說起來是蠻簡單的，但問題就出在：⁴√3要如何求？？我是用電腦算出很精確的近似值再輸入AutoCAD來繪製精確的幾何圖形，但當數值顯示至AutoCAD所能顯示之最大精度時，仍然可看出正方形其中兩邊仍有極小誤差值（如圖2-2-4）。

但是，圖2-2-5是用了一個內冪公式，來得到一段完全為⁴√3長度的幾何線段，精確度百分之百，列在下面供您參照：

如圖示，由A點往下延伸高的二倍，得M點。

以M為圓心，正三角形邊長2為半徑，畫圓，交AM延伸線於P。

找出AP中點Q，以Q為圓心，QP長為半徑，畫圓，與過M之AP垂直線交於O。

由幾何內冪公式可知：AM×MP＝2√3×2＝MO²，則

MO＝2（⁴√3），取MO中點得N，則MN即為⁴√3（正方形之邊長）。

最後，以E為圓心，MN為半徑畫圓，交底邊BC於I，即得正確之正方形之邊長EI。

又如圖2-2-6所示，其為證明：將正三角形以基本分割模式是矩形之分割翻轉四邊形為平行四邊形，而非正方形，如圖示中：

分割翻轉之四邊形邊長：

一為 2DF＝2GH＝3.940891cm

另一為 EI＝IG+GE＝IF+IG＝2GE+GF＝3.982730cm

由上式可知：兩者差距微乎其微，單用肉眼看不清楚，且亦容易遭人誤判，此亦與我的驗證相符合，其推論方法雖和我不同，但殊途同歸，結果正與我的研究成果不謀而合。（下圖2-2-7就是我以它的作圖法重新繪製的正確圖形） 

圖2-2-7

Haberdasher's Problem

圖2-2-8

With three cuts, dissect an equilateral triangle into a square. First proposed by Dudeney (1907) and discussed in Gardner (1961, p. 34), Stewart (1987, p. 169), and Wells (1991, pp. 61-62). The solution can be hinged so that the four pieces collapse into either the triangle or the square. Two of the hinges bisect sides of the triangle, while the third hinge and the corner of the large piece on the base cut the base in the approximate ratio 0.982:2:1.018.

以上是在一美國公司的數學網站上所找到的一份資料，其中提到正三角形分割為正方形的底邊中由右至左的三線段的比，在正三角形邊長為4下，它算出三條線段的比為 0.982：2：1.018，利用AutoCAD的尺寸標註功能，在正三角形邊長為40下，算出更精確的比值9.81969533：20：10.18030467，由9.81969533≠10.18030467更可證明在前面所推出的結論（如圖2-2-2），也就是正三角形分割為正方形是平行四邊形分割法，而不是矩形分割法。

正三角形分割翻轉成四邊形之推演申論

除了上個單元所述，也可依上面的方法設計分割正三角形翻轉成四邊形以及其特定邊長比值或角度極限值之計算，各種不同四邊形包括：（1）矩形（2）菱形（3）平行四邊形（4）梯形（5）任意四邊形，以下就是整理出的各種正三角形分割變化的探討：

1. 預期形狀性質：四角皆直角、兩鄰邊不等長。
2. 基本分割模式：矩形、平行四邊形兩種皆可。
3. 分割頂點位置：基本分割形之兩對角頂點在另一對角線上之垂足。
4. 圖例：




圖2-3-1

5. 說明：由預期形狀之特性，可將分割線與對角線垂直，也就是分割頂點為兩頂點的垂足，如此便可滿足四角垂直的條件，而平行四邊形也可滿足這個條件，如圖2-3-2。




圖2-3-2

6. 特定邊長比值或角度極限值之計算：

1. 預期形狀性質：四邊等長、相鄰兩角不同。
2. 基本分割模式：矩形、平行四邊形兩種皆可。
3. 分割頂點位置：對角線交點、特定點。
4. 圖例：




圖2-3-3

5. 說明：由預期形狀的特性，我可以由矩形對角線互相平分的特點來設計圖形。即使在平行四邊形分割模式下，我也可以在平行四邊分割模式中以作圖的方式來找到可以形成菱形的分割頂點。（如圖2-3-4）首先，我先在AC上任取一點F，使DF為平行四邊形之一對角線，此線必為菱形邊長（JH＝DF），由於菱形四邊等長，故我以E、G為圓心，菱形邊長為直徑，畫圓，分別交DF於H、I兩點，如此2HE＝JH＝HL。故JKLH為菱形。




圖2-3-4

6. 特定邊長比值或角度極限值之計算：

1. 預期形狀性質：兩對角相等、兩對邊等長。
2. 基本分割模式：矩形、平行四邊形。
3. 分割頂點位置：對角線交點、特定點。
4. 圖例： 




圖2-3-6

5. 說 明：由預期形狀的特性我只需達成兩對邊等長即可，故可利用平行四邊形對角線互相平分的特點來作分割頂點（其實矩形分割法也可，只是矩形對角線不但平分且 皆等長，所以它會翻轉成菱形）。另外同樣可以在平行四邊形分割模式或矩形分割模式下，用另一種方法來設計平行四邊形的特定邊長，即是利用兩對邊等長的原 理，以D、F（或G、E）為圓心，希望之平行四邊形邊長為直徑（但DH或GH不可大於GD），畫圓，即可交對角線EG（或DF）於H、I兩點，此兩點即為分割頂點。（如圖2-3-7-A及2-3-7-B）
6. 特定邊長比值或角度極限值之計算：

1. 預期形狀性質：一對邊平行且不等長。
2. 基本分割模式：矩形、平行四邊形。
3. 分割頂點位置：其中一對角線上之特定點。
4. 圖例： 





圖2-3-9 圖2-3-10

5. 說明：由預期頂點的特性，我只要使∠DHL＋∠DJK＝∠DHL＋∠DHG＝180^。即可，因此不管是平行四邊形或矩形，只需分割頂點在一直線上（即∠DHG＋∠DHL＝180^。）都可翻轉成梯形。
6. 特定邊長比值或角度極限值之計算：

1. 預期形狀性質：四角不相等、四邊不等長或不平行。
2. 基本分割模式：矩形、平行四邊形。
3. 分割頂點位置：不在以上所討論的特定點上的其他任意點。
4. 圖例：


圖2-3-11

5. 說明；任意四邊形的分割很簡單，只要分割頂點不在基本分割四邊形的對角線上或邊上即可。

既然我可以設計正三角形分割成各種四邊形，當然也可以逆推正方形分割翻轉成各種三角形。我可以從三角形分割成四邊形的圖形看出，若把基本分割模式的矩形或平行四邊形的LH和MG向上延伸，交得E、F，則EFGH和基本分割模式的矩形或平行四邊形相等（△HIL全等△HJE，△GMK全等△GFJ），即為預期分割四邊形的內接四邊形，且△HJG和△IJK相似。憑著這個道理，我就將一正方形兩邊中點作為基本分割模式中兩點，作成正方形的內接四邊形，於是我便可依此模式設計分割成三角形（圖2-4-1）。由於正方形的基本分割模式和三角形的基本分割模式全等，因此正方形的基本分割模式也有兩種：即矩形分割模式或平行四邊形分割模式。

圖2-4-1

其實原理都大同小異，且有些分割用正三角形來設計不容易，但用正方形逆推就很簡單。

本章節探討的便是正方形分割設計翻轉各種不同三角形，及其特定邊長比值或角度極限值之計算；各種不同三角形包括：（1）正三角形（2）等腰三角形（3）直角三角形（4）不等三角形。正三角形部分已於前面介紹過，其他設計分類如下：

（1）等腰三角形

1. 預期形狀性質：兩邊等長。
2. 基本分割模式：矩形、平行四邊形。
3. 圖例：



圖2-4-2A 圖2-4-2B

4. 說明：因△HJG和△IJK相似，故不論是平行四邊形或矩形基本模式，只要使△HJG其中兩邊相等即可，最簡單的就是做HG中垂線交EF之點即可。(如圖例之J點)
5. 特定高與底之比值與極限值：
1. 矩形基本分割模式：

（2）直角三角形

1. 預期形狀性質：一角直角。
2. 基本分割模式：矩形、平行四邊形。
3. 圖例：(如圖2-4-3A、圖2-4-3B)
4. 說明：做HG過H或G點的垂線交EF之點，使△HJG一角成直角即可。但這種方式在矩形分割模式中(如圖2-4-3B)因矩形兩邊本已垂直，且GH＝GF，故翻出的圖形為等腰直角梯形。

  

圖2-4-3A 圖2-4-3B

1. 特定高與底之比值與極限值：同前（1）等腰三角形之敘述。

（3）不等三角形

1. 預期形狀性質：三邊不等，三角亦不等。
2. 基本分割模式：矩形、平行四邊形。
3. 圖例：




圖2-4-4A 圖2-4-4B

4. 說明：只要將頂點設在EF線段上，且不要與以上所述的點重複即可。
5. 特定高與底之比值與極限值：同前（1）等腰三角形之敘述。

1. 本篇研究範圍包括：正三角形的分割設計，以翻轉出不同四邊 形；以及正方形的分割設計，以翻轉出不同三角形。其實在相同推導原理與模式下，任意三角形皆可設計分割翻轉變形成各種不同四邊形；反之，任一四邊形亦皆可 設計分割翻轉成任一三角形，只是深入研究後，發現題目太大，且有更多的限制條件！這只能留待以後有更充裕的時間來努力或由學弟來接棒了。
2. 正三角形分割四塊拼成正方形之問題，已經證實為世界最少分割塊數，本篇研究即以分割四塊為基礎。其實世界各地皆有許多知名數學家投入研究，並著書立論，單本研究題目就被炒作了一世紀，但是即使發現新的分割法，其分割塊數皆未低於四塊。因此我仍然相信這個問題下一個世紀還會繼續發燒下去！
3. 本研究成果可以：

1. 應用為數學的幾何教材。
2. 以翻轉變形特性製成極富教育意義且有趣之幾何教助模型。
3. 設計成幾何等積變形電腦動畫。
4. 設計製成益智玩具上市，國內外已經有許多幾何分割益智玩具正在販售中（如下圖左）！
5. 還有個令人膾炙的應用，可仿照七巧板之實物應用（如下圖右），設計製作成四件式拼盤或桌子，三角桌供三人坐，四方桌供四人坐，有趣又益智！

1. 除此之外，還存有無數個高難度的幾何分割技巧的類型；例如：正方形分割成十字形、正六邊形、正八邊形、星形…等，幾乎各種多邊形的相互幾何分割變化都有人在研究，甚至也有一些有趣的形狀（如下圖）。其中有一個日本網站更是將之應用的淋漓盡致：他們利用Java語言設計幾何圖形的分割變化模型，供人在網路上模擬操演各式幾何變化情形。這些在在都表示了在幾何分割變形的領域，仍有極大的研究發展空間。





2. 同樣的推導 模式，其實可以演繹到任意三角形皆可設計分割翻轉成任意四邊形；同樣的，任意四邊形也可設計分割翻轉成任意三角形，甚至是任意三角形設計分割翻轉成任意三 角形或任意四邊形設計分割翻轉成任意四邊形；本研究的理論基礎就是都以任意三角形為圖例來說明。雖然因時間因素無法一一贅述，但以上提到的各種分割方法，皆以AutoCAD R14繪成設計簡圖，以供參考。（詳見附錄）

1. 在三角形分割翻轉成四邊形的設計架構中，有矩形和平行四邊形兩種基本分割模式，且兩四邊形之上邊頂點分別為三角形兩邊之中點。
2. 正三角形分割翻轉成正方形理論上可行，也可用幾何作圖方式求出⁴√3的線段以做出真正的分割點。
3. 正三角形在平行四邊形分割模式下分割翻轉成正方形與正三角形在矩形分割模式下分割翻轉成矩形，兩者極難分辨，他們的分割點在邊長50下，只差t=0.22538084而已，且正三角形在矩形分割模式下分割翻轉成矩形，在正三角形邊長50下，矩形兩邊只差0.33920785而已。
4. 正三角形分割為正方形的底邊中由右至左的三線段的比，在正三角形邊長為4下，算出精確的比值為0.981969533：2：1.018030467，與正三角形在矩形分割模式下分割翻轉成矩形的底邊三線段比1：2：1不同。
5. 正三角形可設計分割翻轉變形成各種不同四邊形。其設計方法依矩形分割模式或平行四邊形分割模式以及分割頂點之條件不同而翻轉成不同四邊形包括：（1）矩形（2）菱形（3）平行四邊形（4）梯形（5）任意四邊形。其限制條件導致翻轉四邊形出現特定邊長比值或角度特定值與極限值：（a為正三角形邊長，b、c各為四邊形兩邊長，h為四邊形的高）

（1）矩形：在矩形分割模式下之特定邊長比值 a：b：c＝4：√7：4（√3/√7）。在平行四邊形模式下之極限值邊長比a：b：c＝2：√3：1。

（2）菱形：在矩形分割模式下，特定邊長比值a：b：c＝4：√7：√7。在平行四邊形分割模式下，邊長範圍為a（√7）/4～a（√3）/2；邊長最大極限值比a：b：c＝2：√3：√3。

（3）平行四邊形：在矩形分割模式下，特定邊長比值 a：b：c＝4：√7：（√3/√7～4）。在平行四邊形分割模式下，邊長範圍為b = a～a/2，c = a/2～a（√3）/2；邊長最大極限值比a：b：c＝2：2：√3。

（4）梯形：在矩形分割模式下特定邊長比值a：（b＋c）＝2：√7； a：h＝1：（√3/√7）。
在平行四邊形分割模式下的邊長範圍a：（b＋c）＝1：（1～√3）及a：h＝2：（√3～1）

6. 正方形可設計分割翻轉變形成各種不同三角形。其設計方法依矩形分割模式或平行四邊形分割模式以及分割頂點之條件不同而翻轉成不同三角形包括：（1）等腰三角形（2）直角三角形（3）任意三角形。其限制條件導致翻轉三角形出現特定高與底之比值或角度特定值與極限值。（其中，a為正方形邊長、m為三角形底邊、h為三角形的高）
1. 在矩形分割模式下的邊長比a：m：h＝1：√2：√2。（即底＝高）
2. 在平行四邊形分割模式下的範圍：2a＞h＞a（2/√5）；a＜m＜a（√5）。 
7. 同樣的推導模式，一樣可以得到：
1. 任意三角形皆可設計分割翻轉成各種四邊形。
2. 任意四邊形皆可設計分割翻轉成各種三角形。
3. 任意三角形皆可設計分割翻轉成其他各種三角形。
4. 任意四邊形皆可設計分割翻轉成其他各種四邊形。

參考資料

1. 清大數學系全任重教授的幾何網站Geometric Construction
2. 幾何作圖
3. http://poncelet.math.nthu.edu.tw/chuan/
   
4. 分割問題
5. The Puzzle World of Polyhedral Dissections By Stewart T. Coffin
 
6. Dissection
 
7. Haberdasher's Problem
8. Congruent Transformation
 
9. Dissections de polygones
 
10. Triangle - Carre (Gif anime Aller-retour)
 
11. 等積變形
 
12. Specials Puzzle Page
 
13. Triangle to Square
14. 
    
Swing-hinged dissection of triangle to square

15. Triangle to Square 討論區
    
16. 蔣聲著，〝幾何變換〞，凡異出版社，p47~60，1994.3
 
17. 談詳柏、張景中編，〝數學遊戲大觀〞，謙謙出版社，p88~94，1991.8
 
18. 張潤青等編，〝數學萬花筒〞，謙謙出版社，p47、p142，1990.12
 
19. 斯坦因豪斯著、裘光明譯，〝數學萬花鏡〞，上海教育出版社，1981
 
20. 林龍震著，AutoCAD R14中文版使用手冊，松崗電腦圖書公司，1997.